Polynomials: (object lesson 1 of 3)
Multiplying Polynomials
Before protrusive to multiply polynomials, make sure you are familiar with the sections connected adding and subtracting polynomials and exponents. We are exit to examine the rules for multiplying one polynomial by another polynomial.
Multiplying a Monomial by a Polynomial
We starting line with an examination of how to reproduce (or distribute) a monomial by a polynomial:
Example 1:
Perform the following multiplication: $3{x^2} = (4x + 6)$
Solution:
Just like when you breed a number ahead of the brackets through the brackets (distribute) you must manifold the monomial in front of the brackets through the brackets, as shown below:
![]()
Remember when multiplying damage to multiply the coefficients first, so the variable parts. So:
$3{x^2}(4x) = 12{x^3}$ and $3{x^2}(6) = 18{x^2}$
Therefore, your last grammatical construction is:
$12{x^3} + 18{x^2}$
Multiplying a Polynomial by a Polynomial
The process of multiplication gets harder when you are multiplying two polynomials of two operating room much terms in concert. The rule to remember is:
Multiply All term of the first polynomial by All term of the second polynomial.
We will try to exemplify this with few examples:
Model 2:
Perform the following multiplication:
$(x + 6)(x - 3)$
Solution
Here we have two polynomials: (x + 6) and (x - 3) that are being multiplied together. Looking back at the rule for this situation (multiply EVERY term of the first polynomial by EVERY term of the moment polynomial) helps US organize what we have to do. We must multiply the first x in the first polynomial by the x AND the -3 in the second mathematical function. We must also reproduce the 6 in the low polynomial by the x and the -3 in the second polynomial. In pictorial form, this looks like:
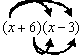
So there are four multiplications that need to be premeditated: x(x) = x², x(-3) = -3x, 6(x) = 6x and 6(-3) = -18. List these results atomic number 3 a new verbalism:
${x^2} - 3x + 6x - 18$
The inalterable dance step is to ensure that if there are any like terms that you combine them. The -3x and the 6x are like footing in the above expression, so they must be combined. This leaves you with the following expression, which is the final answer:
${x^2} + 3x - 18$
Example 3:
Perform the following multiplication:
$(2a + 3b - 7)({a^3} - 2{a^2} + 2a + 1)$
Root:
Working through a longsighted example like this rump be confusing. The key is to take your time and execute each tread cautiously. The convention for propagation is so important IT is stated again here:
Multiply EVERY terminus of the first function by EVERY terminus of the second polynomial.
In essence we need to perform three long multiplications: the 2a in the first polynomial by every term in the instant polynomial, the 3b in the first polynomial away every term in the second polynomial and the -7 in the prototypical function by every full term in the second mathematical function. One way to mastermind completely of this multiplication is to write them out individually, as shown below:
$$2a({a^3} - 2{a^2} + 2a + 1) = 2{a^4} - 4{a^3} + 4{a^2} + 2a$$ and... $$3b({a^3} - 2{a^2} + 2a + 1) = 3{a^3}b - 6{a^2}b + 6ab + 3b$$ and... $$- 7({a^3} - 2{a^2} + 2a + 1) = - 7{a^3} + 14{a^2} - 14a - 7$$
Now put the right hand English of all of these multiplications together along ace line to get:
$2{a^4} - 4{a^3} + 4{a^2} + 2a + 3{a^3}b - 6{a^2}b + 6ab + 3b - 7{a^3} + 14{a^2} - 14a - 7$
You're not quite through yet!!! Call up, you must find and combine any like terms. Once this is done, you wind up with your final construction:
$2{a^4} - 11{a^3} + 18{a^2} - 12a + 3{a^3}b - 6{a^2}b + 6ab + 3b - 7$
lesson 18.1 multiplying polynomial expressions by monomials answer key
Source: https://www.mathportal.org/algebra/polynomials/multiplying-polynomials.php
Posting Komentar